RESEARCH INTERESTS

Modified gravity

I am interested in modified theories of gravity. A variety of modified gravity theories have been analysed and it was found that some of these models satisfy cosmological and local gravity constraints and are practically indistinguishable from the ΛCDM model, at least at the background level. There many generalisations and modifications of the Einstein-Hilbert action. For instance, an arbitrary function of the Gauss-Bonnet term in the action yields additional terms in the resulting field equations. Likewise, higher order terms, including squares of the Ricci tensor, the Riemann tensor and the Weyl tensor lead to interesting models.

At the moment I am particularly interested in studying metric-affine theories of gravity which are based on the Einstein-Hilbert action

  S = ∫ R(g,Γ) √  -g   d4x

where the metric g and the connection Γ are regarded as independent dynamical variables. In this approach to gravity, we can recover General Relativity by choosing the connection to be the Levi-Civita connection. However, this theory is much more general as the connection couples differently to the matter. For instance, Fermions act as sources to the skew-symmetric part of the connection.

Continuum mechanics

I am mainly interested elasticity with microrotations, also known as Cosserat elasticity or micropolar elasticity. This field shows some surprising similarities with general relativity. For instance, microrotations can be described using concepts from differential geometry, in particular the torsion tensor. It turns out that the action of microrotations looks like a three-dimensional version of the action of teleparallel gravity. In this context we could find some travelling wave solutions. In these animations the linear movements of the rings indicate the effect of elastic displacements while the rotations indicate the microrotations at these points.

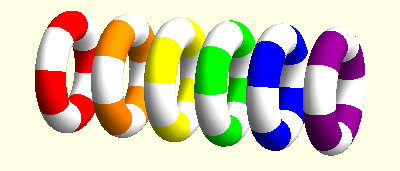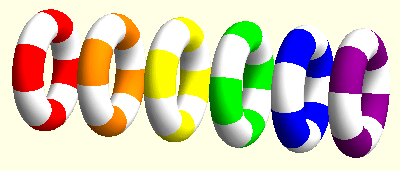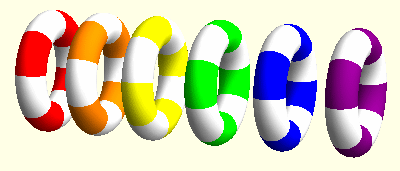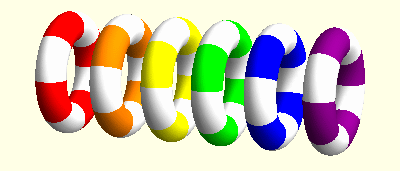
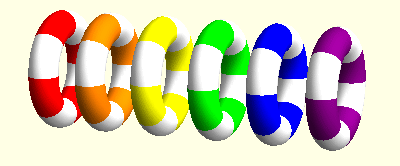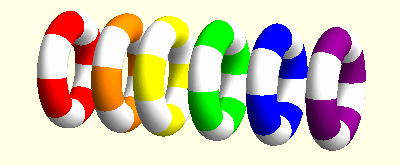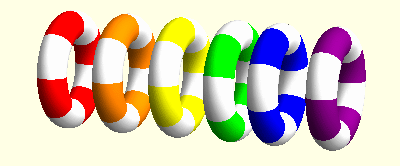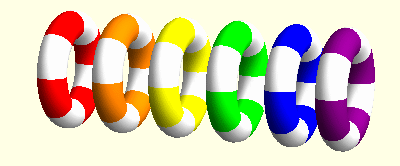
The animation shows a longitudinal elastic wave and a longitudinal rotaional wave. Courtesy of Belgin Seymenoglu.
This figure shows a longitudinal soliton. Courtesy of Belgin Seymenoglu.

Spinors in gravitation and cosmology

Since late 2005 I have been working on non-standard spinors. In two of my papers I formulated their theory on a curved manifold and laid the foundations to investigate their possible role in cosmology. I could further prove that spin 1/2 particles based on the non-standard spinors do not necessarily yield an axially symmetric torsion tensor. Together with David Mota, we were able to show that indeed an inflationary scenario with these spinors has the effect of suppressing the low multipole amplitude of the primordial power spectrum. With James Burnett we were able to solve one of the open problems in Einstein-Cartan theory, namely we find that dark spinors are a natural matter source whose spin angular momentum tensor is compatible with the cosmological principle.

Spherically symmetric gravity

Exact solutions of the Einstein field equations in the spherically symmetric case have always been a major field of my research. I already constructed five new global solutions. I could further extend my results to include anisotropic stresses and charges. This has recently stimulated new research in this direction from a more mathematical point of view, most notably by Håkan Andreasson who introduced some new techniques to analyse the field equations. I would like to examine the possibilities of these new techniques in particular in the presence of the cosmological constant. Because of the more complex asymptotic structure of spacetime it is not clear at the moment if these techniques can yield further results.